Design Turbulence
The site-specific design equivalent turbulence is used to determine whether the turbine type selected for the wind farm is suitable and operates within its design parameters.
Introduction
From the definition of the mean wind speed, turbulence is defined as all wind fluctuations with periods less than the averaging period. One common measure of turbulence is the turbulence intensity - defined as:
$$I = \frac{\sigma_{v}}{\bar{v}}$$
where
σv standard deviation of wind speed v in the averaging period
${\bar{\sigma}}_{i,j}$ mean wind speed in the averaging period
The same notation is used here as in the relevant IEC Standards [21], [22]. Both values must be determined from the same set of measured data samples of wind speed. The typical averaging period is 10 min.
When a set of turbulence intensity measurements is taken over a period, it is possible to plot all the single values of turbulence intensity as a function of the single measured mean wind speeds $\overset{\bar{}}{v}$. The plot may look like this:
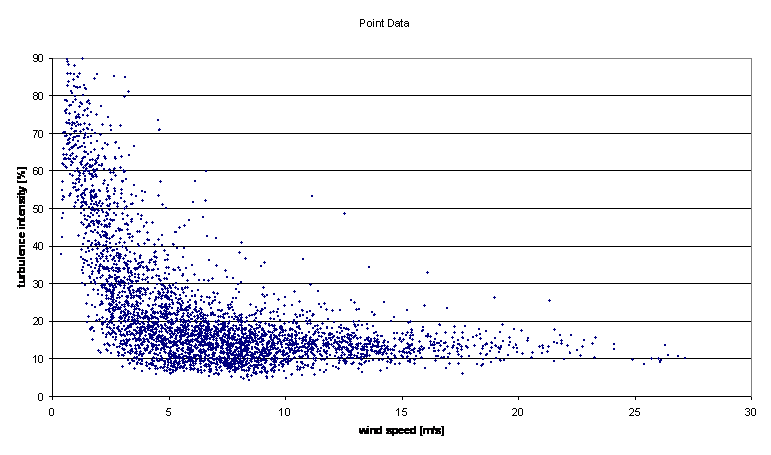
Measured turbulence intensities as a function of the mean wind speed over the averaging period
For every wind speed bin, a mean turbulence intensity is calculated from the single values. With regard to turbine loads, single turbulence intensities greater than the mean value are more relevant. To analyse these, it is assumed that all the single values within a wind speed bin have a normal distribution, with a mean value and a standard deviation that can be calculated from the sample data in the specific bin. In terms of turbine loads, specific quantiles of the turbulence intensity distribution are used, depending on the definition in the design standards.
Values used in the standards are:
Characteristic value: mean turbulence intensity plus one standard deviation. This represents the 84% quantile of a normal distribution, which means that 84% of the data are smaller than, or equal to, the characteristic value.
Representative value: mean turbulence intensity plus 1.28 times the standard deviation. This is the 90% quantile of a normal distribution, which means that 90% of the data are smaller than, or equal to, the representative value.
The Mean, Characteristic and Representative turbulence intensities are marked in the figure below, for specific wind speed bins.
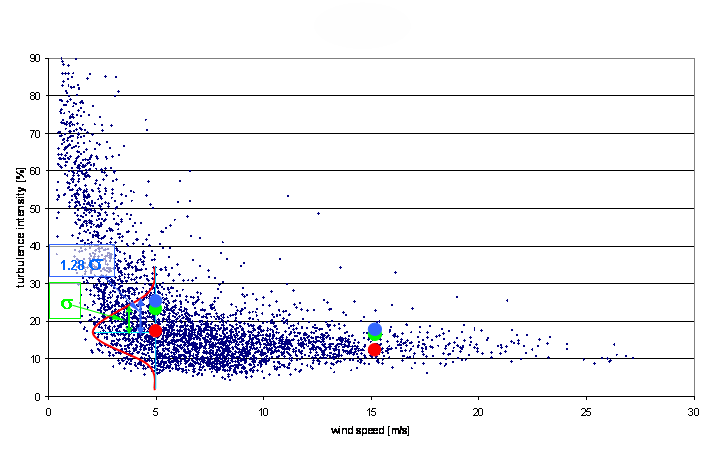
Mean (red), Characteristic (green) and Representative (blue) turbulence intensities of turbulence measurements
Design Standards
The assessment of structural integrity of wind turbines is done via comparison of the site- specific wind parameters at the wind turbine site with those used for the design. There are different design standards that define the wind conditions a wind turbine shall be designed to withstand, in different ways.
Using WindFarmer, design turbulence estimates can be produced with respect to the following design standards
IEC 61400-1:1998 (Edition 2)
IEC 61400-1:2005 (Edition 3)
IEC 61400-1:2005/A1:2010
DIBt
The design turbulence definitions in these standards and the methods used in WindFarmer to calculate the site-specific design turbulence, are given in the following sections.
For calculation of design turbulence estimates, turbulence intensity values measured at the site masts are input in the Calculate Wind Climate task. It is important not to input Characteristic or Representative turbulence values here. Values for the standard deviation of wind speed standard deviation, known as “sigma-sigma”, can be calculated directly from the measured time series data in WindFarmer when time series data of mean wind speed and wind speed standard deviation are available.
The calculations of Effective turbulence estimates are designed for use with the Modified PARK wake model.
The turbulence intensity outputs from the Eddy Viscosity wake model of WindFarmer are true meteorological turbulences. They should not be compared directly with the IEC or DIBt turbulence models.
IEC 61400-1, Edition 2
In this Standard [22] the design turbulence is defined as a “Characteristic” value.
The maximum allowed Characteristic turbulence is defined according to the turbine class. The Characteristic turbulence and the longitudinal wind velocity standard deviation σ1 are linked through the following formula:
Equation 2
$$\sigma_{1}\left( v_{h\textrm{ub}} \right) = \frac{I_{15}\left( 15 + a \cdot v_{h\textrm{ub}} \right)}{\left( a + 1 \right)}$$
where
σ1 is in this case called the Characteristic value of the standard deviation of the longitudinal wind speed component
I15 is the characteristic value of the turbulence intensity at 15m/s
a is the slope parameter
vhub is the wind speed at hub height in m/s
The parameters I15 and a are specified in the standard according to the turbulence level of the turbine class. For low turbulence (I15, a) = (0.16, 3) and for high turbulence (I15, a) = (0.18, 2).
The standard does not state how wake effects at the site may be taken into account in the calculation of the site-specific characteristic turbulence. One method how to do this is published in [23], whereby the wake effects from neighbouring turbines are considered by an Effective turbulence. The Effective standard deviation is defined as
$${\sigma_{ch\textrm{ar}}}_{i,j} = {\overset{\bar{}}{\sigma}}_{i,j} + {\sigma_{\sigma}}_{i,j}$$
where
${\overset{\bar{}}{\sigma}}_{i,j}$ is the probability of the wind speed bin i and the wind direction bin j. In WindFarmer the predicted turbine-specific probability is used.
m is the Wöhler coefficient representative for the turbine and component receiving turbulence.
The Wöhler coefficient is specific to component material and geometry and is derived from the slope of the log-log plot of the S-N curve (magnitude of a cyclical stress (S) against the cycles to failure (N)), where the relation S ∝ N-1/m is assumed. Typical values for wind turbines range between 3 and 15 where 4 is appropriate for simple steel components and values 10 to 15 are suitable for simple composite components. The turbine manufacturer should be consulted for advice on an acceptable range of Wöhler indices for these calculations.
The estimate of a site specific effective turbulence can be expressed following [23] as:
Equation 3
$${\sigma_{\textrm{eff}}}_{i,j} = \sqrt{\frac{v_{hub,i}^{2}}{(1.5 + 0.3 \cdot d_{j} \cdot \sqrt{v_{hub,i}})^{2}} + {\sigma_{ch\textrm{ar}}}_{i,j}^{2}}$$
where
dj is the distance to the neighbouring turbine that causes the wake in direction bin j normalised by the rotor diameter of the turbine causing the wake.
σchar i,j is the characteristic ambient wind speed standard deviation in wind direction bin j and wind speed bin i
As an option the actual thrust coefficient can be used instead of the approximation given above. vhub is then replaced by 7/ct.
For wind directions where there are no upstream turbines or turbine distances greater than 10 rotor diameters σeff i,j = σchar i,j.
With these definitions $\sigma_{\textrm{eff}}(v_{hub,i})$ represents the Characteristic value of the wind speed standard deviation.
The estimate of the Effective turbulence Ieff is calculated in WindFarmer for all wind speeds and directions and is available as output in the Flow and Performance Matrix.
The characteristic wind speed standard deviation is defined as
$${\sigma_{ch\textrm{ar}}}_{i,j} = {\overset{\bar{}}{\sigma}}_{i,j} + {\sigma_{\sigma}}_{i,j}$$
where
$${\overset{\bar{}}{\sigma}}_{i,j}$$ is the mean of wind speed standard deviation in wind direction bin j and wind speed bin i
σσi, j is the standard deviation of wind speed standard deviation in wind direction bin j and wind speed bin i (“sigma-sigma”)
If σσi, j is not available from measurements it can be assumed [6.3] that it is 20% of the mean wind speed standard deviation, so that
$${\sigma_{ch\textrm{ar}}}_{i,j} = 1.2 \cdot {\overset{\bar{}}{\sigma}}_{i,j}$$
The corresponding estimate of the Characteristic turbulence intensity $\frac{\sigma_{\textrm{eff}}\left( v_{hub,i} \right)}{v_{hub,i}}$ as a function of wind speed is available in the Flow and Performance Matrix of WindFarmer.
To get a measure of the suitability of a wind turbine for the site, the wind turbine should satisfy the condition that the estimated Characteristic value of the turbulence standard deviation σ1 (Equation 2) shall be greater than or equal to σeff at hub height wind speeds vhub within the operational range of the turbine.
IEC 61400-1, Edition 3
In this Standard [21] the design turbulence is defined as a “Representative” value.
The maximum allowed turbulence is defined according to the turbine class. The expected value of the hub height turbulence intensity at a 10-min average wind speed of 15m/s and the turbulence standard deviation σ1 are linked through the following formula:
Equation 4
$$\sigma_{1}\left( v_{h\textrm{ub}} \right) = I_{\textrm{ref}}\left( 0.75 \cdot v_{h\textrm{ub}} + b \right)$$
where
σ1 is in this case called the representative value of the standard deviation of the longitudinal wind speed component
Iref is the mean value of the turbulence intensity at 15 m/s
b 5.6 m/s
vhub is the wind speed at hub height in m/s
The parameter Iref is specified in the standard according to the turbulence level of the turbine class. For low turbulence Iref is 0.12, for medium turbulence it is 0.14 and for high turbulence 0.16.
The wake effects from neighbouring turbines can be taken into account by an effective turbulence which, according to the standard, may be derived using a Frandsen method. The Effective turbulence estimate is defined as
$$\sigma_{\textrm{eff}}(v_{hub,i}) = \left( \sum_{j}^{}{P_{i,j} \cdot {\sigma_{\textrm{eff}}}_{i,j}^{m}} \right)^{1/m}$$
where
Pj is the probability of the wind speed bin i and the wind direction bin j. In WindFarmer the predicted turbine- specific probability is used.
m is the Wöhler coefficient.
The Wöhler exponent is specific to component material and geometry and is derived from the slope of the log-log plot of the S-N curve (magnitude of a cyclical stress (S) against the cycles to failure (N)), where the relation S ∝ N-1/m is assumed. Typical values for wind turbines range between 3 and 15 where 4 is appropriate for simple steel components and values 10 to 15 are suitable for simple composite components. The turbine manufacturer should be consulted for advice on an acceptable range of Wöhler indices for these calculations.
Within WindFarmer, the site-specific Effective turbulence estimate derived from the Frandsen method is expressed as:
Equation 5
$${\sigma_{\textrm{eff}}}_{i,j} = \sqrt{\frac{0.9 \cdot v_{hub,i}^{2}}{(1.5 + 0.3 \cdot d_{j} \cdot \sqrt{v_{hub,i}})^{2}} + {\overset{\bar{}}{\sigma}}_{i,j}^{2}}$$
where
dj is the distance to the neighbouring turbine that causes the wake in direction bin j normalised by the rotor diameter of the turbine causing the wake
$${\overset{\bar{}}{\sigma}}_{i,j}$$ is the mean ambient wind speed standard deviation in wind direction bin j and wind speed bin i
WindFarmer provides an option to use the actual thrust coefficient instead of the approximation used in the standard. vhub in the denominator is then replaced by 7/ct.
For wind directions without upstream turbines or turbine distances greater than 10 rotor diameters
σeff\ i,j = ${\overset{\bar{}}{\sigma}}_{i,j}$
The estimate of the Effective turbulence intensity Ieff is calculated in WindFarmer for all wind speeds and directions and is available in the Flow and Performance Matrix.
The representative value of wind speed standard deviation σrep is defined as the 90% quantile of the turbulence standard deviation
σrepi = σeff(vhub, i)+1.28σσi
where
${\sigma_{\sigma}}_{i}$ is the standard deviation of wind speed standard deviation in wind speed bin i, given as a mean over all wind directions
If ${\sigma_{\sigma}}_{i}$ is not available from measurements, it can be assumed that it is 20% of the mean wind speed standard deviation [22], so that
$${\sigma_{\textrm{rep}}}_{i} = \sigma_{\textrm{eff}}(v_{hub,i}) + 0.256{\overset{\bar{}}{\sigma}}_{i}$$
where
${\bar{\sigma}}_{i}$ is the mean of standard deviation of ambient wind speed in wind speed bin i, given as a mean over all wind directions
The corresponding Representative turbulence intensity $\frac{{\sigma_{\textrm{rep}}}_{i}}{v_{hub,i}}$ is available in the Flow and Performance Matrix of WindFarmer.
To get a measure of the suitability of a wind turbine for the site, a wind turbine should satisfy the condition that the estimate of the representative value of the turbulence standard deviation σ1 (Equation 4) shall be greater than or equal to σrep at hub height wind speeds vhub between 0.2 vref and 0.4 vref of the turbine, with vref the reference wind speed of the turbine class defined in the standard. When the turbine properties are known, it is adequate to verify this for hub height wind speeds between 0.6 rated wind speed and cut-out wind speed.
IEC 61400-1, Edition 3, Amendment
The amendment to IEC 61400-1 Edition 3 [24] introduces the following key changes for calculating an estimate of the effective design turbulence:
The site-specific Effective turbulence estimate derived from the Frandsen method is expressed as:
Equation 6
$${\sigma_{\textrm{eff}}}_{i,j} = \sqrt{\frac{v_{hub,i}^{2}}{\left( 1.5 + 0.8 \cdot \frac{d_{j}}{\sqrt{c_{t}}} \right)^{2}} + {\sigma_{\textrm{rep}}}_{i,j}^{2}}$$
where
dj is the distance to the neighbouring turbine that causes the wake in direction bin j normalised by the rotor diameter of the turbine causing the wake
${\sigma_{\textrm{rep}}}_{i,j}$ is the representative ambient wind speed standard deviation in wind direction bin j and wind speed bin i
ct is the turbine thrust coefficient of the upwind turbine at wind speed vhub,i
Optionally the thrust coefficient or an approximation of the actual thrust coefficient can be used. ct is then replaced by 7/vhub.
For wind directions without upstream turbines or turbine distances greater than 10 rotor diameters $σrep i,j = {\bar{\sigma}}{i,j} + 1.28{\sigma{\sigma}}_{i,j}$. Please note that this term is calculated in the amendment as part of Equation 6 rather than applied afterwards.
- DIBt
The calculation method defined in [23] must be read in conjunction with the DIBt Standard [25]. In the Standard [25], the design turbulence is defined as a “Characteristic” value. In general, the maximum turbulence allowed, defined according to the turbine class, is equivalent to the definition in IEC 61400-1 (Edition 2). The calculation method for site specific design equivalent turbulence intensity is defined in [25], similar to the method used in the WindFarmer calculation according to IEC 61400-1 (Edition 2). But, contrary to the IEC 61400-1 (Edition 2) calculation, the thrust coefficient is not replaced by the approximation (7m/s)/vhub, as proposed in [23]. The site-specific effective turbulence is defined by
$${\sigma_{\textrm{eff}}}_{i,j} = \sqrt{\frac{v_{hub,i}^{2}}{\left( 1.5 + 0.8 \cdot \frac{d_{j}}{\sqrt{c_{t}}} \right)^{2}} + {\sigma_{ch\textrm{ar}}}_{i,j}^{2}}$$
Where
dj is the distance to the neighbouring turbine that causes the wake in direction bin j normalised by the bigger of the rotor diameters
ct is the turbine thrust coefficient of the upwind turbine at wind speed vhub,i
WindFarmer provides an option to use the actual thrust coefficient instead of the approximation used in the standard. vhub is then replaced by 7/ct.
The general calculation methodology is equivalent to that described for IEC 61400-1 (Edition 2).
Large wind farm turbulence correction
The ambient turbulence level increases within large wind farms. An adjustment has been suggested when the number of wind turbines from the receiving wind turbine to the ‘edge’ of the wind farm is more than 5, or the spacing in the rows perpendicular to the dominant wind direction is less than 3 rotor diameters [21].
In this case ${\overset{\bar{}}{\sigma}}_{i,j}$ is replaced by ${\overset{\bar{}}{\sigma}}_{i,j}^{'}$, which is
$${\overset{\bar{}}{\sigma}}_{i,j}^{'} = \frac{1}{2}\left( \sqrt{\sigma_{w}^{2} + {\overset{\bar{}}{\sigma}}_{i,j}^{2}} + {\overset{\bar{}}{\sigma}}_{i,j} \right)$$ with
$$\sigma_{w} = \frac{0.36 \cdot v_{hub,i}}{1 + 0.2\sqrt{\frac{d_{r} \cdot d_{t}}{c_{t}}}}$$
where
ct is the turbine thrust coefficient of the upwind turbine at wind speed vhub,i
dr is the turbine separation within rows in rotor diameters
dt is the turbine separation between rows in rotor diameters
The correction is applied for wind directions with a wake from an upstream turbine for IEC Edition 2, IEC Edition 3 and DIBt. WindFarmer approximates dr, and dt for all layouts to be the distance to the closest neighbouring turbine and the distance to the upstream turbine causing the wake.
In the calculations according to IEC Edition 3 Amendment the correction is applied for wind directions without a wake from an upstream turbine. The thrust coefficient is then that of the turbine under consideration.
WindFarmer approximates dr, and dt for all layouts to be the distance to the closest neighbouring turbine and the distance to the 3rd closest turbine.
If this correction is selected by the user, it is applied to all wind directions whether or not the number of wind turbines from the receiving wind turbine to the ‘edge’ of the wind farm is more than 5, or the spacing in the rows perpendicular to the dominant wind direction is less than 3 rotor diameters.
Simple and Advanced approach
The calculations models given in the Design Standards are intended for use in wind farms with a regular turbine layout. The model described in [23] has been derived for wind farms in simple terrain and consisting of just one turbine type. In many cases, wind turbines are not in a regular layout, they are located in complex terrain and there are also different turbine types at the wind farm. Some assumptions have been made to take this into account. On the other hand, a simple approach has also been made, which is called the 'Simple Model' in WindFarmer. Differences between the Advanced and Simple models are explained below.
Depending on the circumstances either the Simple or the Advanced model may give more conservative results.
Direction sectors with increased turbulence
To implement the above, it is necessary to identify the wind direction sectors in which a turbine will experience increased loads due to the wakes of upstream turbines. These sectors are determined by applying the approach proposed in [23]. Effective turbulence is calculated using Equation 3, Equation 5 or Equation 6 as soon as a part of the rotor is within the wake of an upstream turbine as represented by a view angle θw.
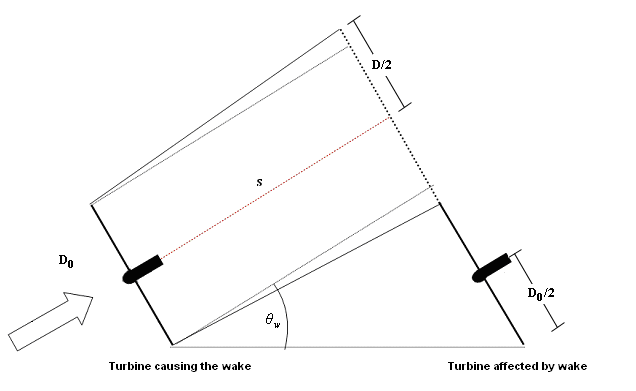
Definition of the view angle θw. D0 is the rotor diameter of the turbines and D is the diameter of the wake at downstream distance s.
The view angle can be described as
$$\theta_{w} = \arctan\left( \frac{1}{s} + k \right)\backslash n$$
where
s is the downstream distance in rotor diameters
k is the wake decay constant
which, following recommendations of [23], is derived on the basis of the linear wake expansion equations of the PARK model.
With k = 0.087, the view angle becomes
Equation 7
$$\theta_{w} = \frac{1}{2}\left( 2\arctan\left( \frac{1}{s} \right) + 10º \right)$$
Also in [23] (equation 3.18) a ‘characteristic view angle’ is defined as:
Equation 8
$$\theta_{w} = \frac{1}{2}\left( \arctan\left( \frac{1}{s} \right) + 10º \right)$$
Equation 7 is used in the advanced model while Equation 8 is used in the simple model.
Both definitions of the view angle comply with IEC61400-1 Ed.3 and are compared in the figure below (k = 0.087):

The area that a downstream turbine can be placed without being exposed to increased load due to the wake of an upstream turbine when using Equation {6.4.3} (red) and Equation {6.4.2} (green). The area shaded in grey represents the wake behind the upstream turbine. The bold red and green lines represent the rotor edge.
In both cases it is assumed that the wake angle is measured downstream from the rotor centre of the turbine that generates the wake. The figure illustrates the area where a downstream turbine can be placed without being exposed to increased load due to the wake of an upstream turbine. It can be seen that when using Equation 8 the downstream turbines can be placed so that half the rotor is within the wake without getting any increase in load whereas when using Equation 7 the load increases as soon as a part of the rotor is within the wake.
The model given by Equation 8 should only be used for calculation of wake turbulence aggregated over a complete wind rose since it can produce non-conservative turbulence estimates for individual wind directions at close spacing.
Other model assumptions
For several upstream turbines the Simple model considers only direct wake effects i.e. the upstream turbines are never considered themselves to be in a wake. The Advanced model considers direct and indirect wake effects of all upstream turbines on all downstream turbines.
The differences in free wind speed due to the terrain are considered in the Advanced model while the same free wind speed at all turbine locations is assumed in the Simple model.
If a turbine thrust coefficient is used, then in the Simple model it is assumed that the thrust coefficient of the turbine causing the wake is the same as for the turbine receiving the wake. In the Advanced model the actual thrust coefficient of the upstream turbine is used in the calculation.
In both models the hub heights of the turbines are considered when determining if the turbine rotor is completely below or above the wake of an upstream turbine so that there is no wake effect. As soon as the tip of the downwind turbine gets into the wake, it is assumed that the turbine has the same hub height as the upstream turbine and how much of the rotor is in the wake is determined. Afterwards, the analysis described in chapter 11.4.1 is carried out.
Wind speed and sector management
During the calculation of the design equivalent turbulence, the program checks whether the turbine under consideration is operational or not, considering the cut-in and cut-out wind speeds and sector management, and using the incident wind speed, including any wake effects. If the turbine is not in operation, the design equivalent turbulence is set to zero.
Evaluation
After deriving the estimates of Characteristic or Representative Turbulence intensity for a particular turbine, they can be compared with the allowable values over the operational wind speed range of the turbines. It should be noted that the allowed wind speed standard deviations σ1(vhub) defined in the design standards must be divided by the hub height wind speed for direct comparison with the Flow and Performance Matrix output of WindFarmer. This is because WindFarmer provides outputs of turbulence intensity and not wind speed standard deviation.
If there are any doubts concerning the suitability of the turbine, a site-specific load calculation should be considered.