Wind shear analysis

Our wind shear analysis tools allow you to calculate a shear model for a measurement site based on time series inputs at multiple heights, then extrapolate wind speed time series to turbine hub heights using this model.

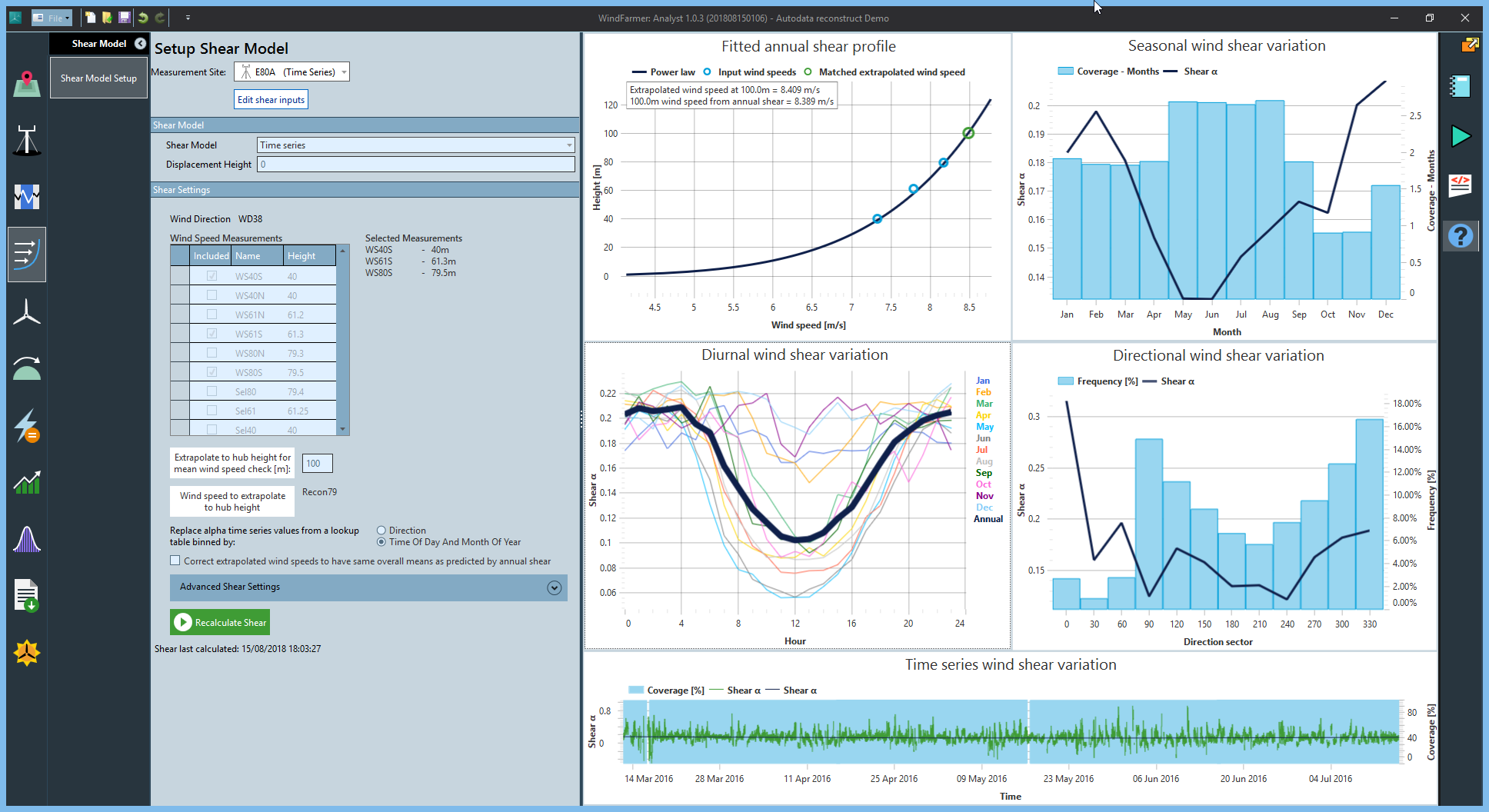
Wind speed extrapolation using a shear model

The extrapolation of a single time series record from one height to another (e.g. mast to hub) is either performed using either the power law or log law:

Log law extrapolation

A surface roughness length z₀ is defines the log law shear model. The speed-up factor between mast height and hub height is calculated as follows:

$$\frac{ U_{hub} }{ U_{mast} } = \frac{ \ln{ \left( \frac{z_{hub} - d}{z_{0}} \right) }}{\ln{ \left( \frac{z_{mast} - d}{z_{0}} \right)}}$$

Power law extrapolation

The power exponent, alpha, is the input parameter. The speed-up factor between mast height and hub height is calculated as follows:

$$\frac{U_{hub}}{U_{mast}} = \left(\frac{z_{hub} - d}{z_{mast} - d}\right)^{\alpha}$$

Fitting the shear model to data

The shear model parameters are calculated from wind speed measurements at multiple heights, using a least-squares fitting method.

When using the power law model, the shear parameter α is calculated from:

$$\alpha = \frac{N\sum_{i}^{}{\ln\left( z_{i} - d \right)\ln\left( u_{i} \right)} - \sum_{i}^{}{\ln\left( z_{i} - d \right)\sum_{i}^{}{\ln\left( u_{i} \right)}}}{N\sum_{i}^{}\left( \ln\left( z_{i} - d \right) \right)^{2} - \left( \sum_{i}^{}{\ln\left( z_{i} - d \right)} \right)^{2}}$$

Where

z_i – measurement height i in m

d – displacement height in m

u_i – wind speed at height i in m/s

N – number of measurement heights

When using the log law model, the shear parameter z₀ is calculated from:

$$\mathrm{\textrm{slope}} = \ \frac{N\sum_{i}^{}{u_{i}*ln\left( z_{i} - d \right)} - \ \sum_{i}^{}{\ln\left( z_{i} - d \right)\sum_{i}^{}u_{i}}}{N\sum_{i}^{}{\ln\left( z_{i} - d \right)} - \sum_{i}^{}{\ln\left( z_{i} - d \right)\sum_{i}^{}u_{i}}}$$

$$\mathrm{\textrm{offset}} = \frac{1}{N}\ \left( \sum_{i}^{}u_{i} - slope*\sum_{i}^{}{\ln\left( z_{i} - d \right)} \right)$$

$$z_{0} = exp\left( - \frac{\mathrm{\textrm{offset}}}{\mathrm{\textrm{slope}}} \right)$$