Long term adjustment

WindFarmer: Analyst includes the ability to calculate and apply a long‑term adjustment to site wind speeds. We calculate a target long-term wind speed at measurement height. When combined with the overall shear from a shear model this measurement height long term wind speed can define a long-term hub-height wind speed which we scale our calculated hub-height wind climate data to.

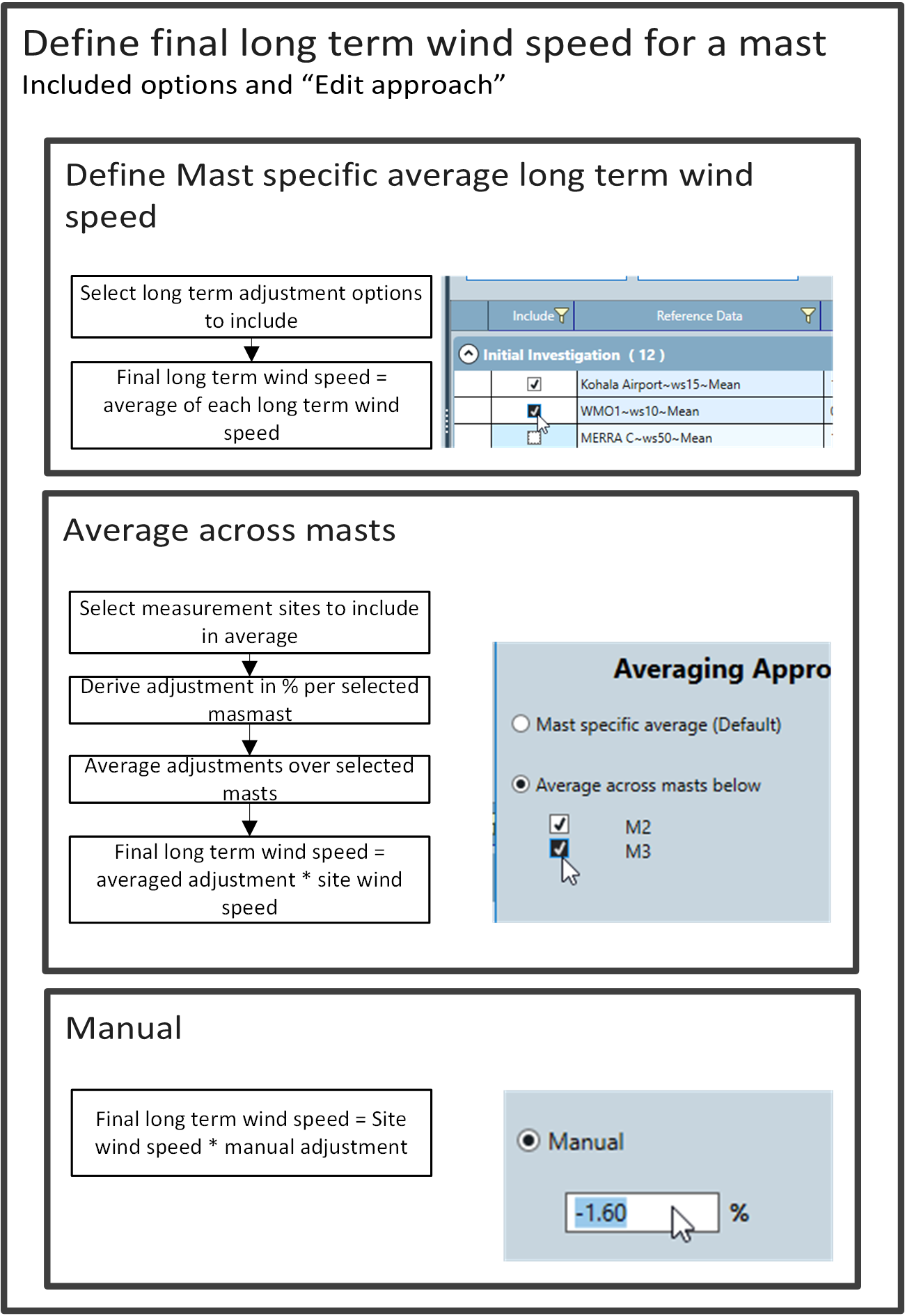
The long-term wind speed is predicted using reference wind speed data, resampling reference and site wind speed records to N‑daily or monthly sampling intervals then applying a linear regression model to derive speedups.

Configurable settings include the ability to force the correlation through the origin or not, the resampling period in days, the minimum coverage for accepting a point in a correlation and the minimum coverage ratio for splicing synthetic site data in to the site data time series to calculate the long term mean wind speed. The long term wind speed calculation for a single pair of site and reference wind speed measurements is shown below:

Combine long term predictions from multiple sources

To derive a long-term measurement-height wind speed considering multiple sources of reference data we average the predicted long term wind speeds from each selected reference data option.

You can further edit the approach to average adjustment predictions at each mast across selected site masts that you believe should have the same long term adjustment, or enter your own manual adjustments following the process described below.

Note

Where site mean wind speeds are used they are always calculated directly from the time series – not the resampled versions of that data.

Long term wind speed uncertainty

WindFarmer calculates three types of uncertainty: variability, consistency and synthesis uncertainty and combines these using the below formulae to obtain the total uncertainty associated with the long term wind speed adjustment obtained from each source of reference data.

$$\sigma_{LongTermWS} = \sqrt{
\left( \frac{IAV}{\sqrt{NYears_{Spliced}}}\right)^2 + \left( \sigma_{Consistency} \frac{NYears_{Spliced}-NYears_{Site}}{NYears_{Spliced}} \right)^2 + \left( \sigma_{Synthesis} \frac{NYears_{Spliced}-NYears_{Site}}{NYears_{Spliced}} \right)^2 } $$

Variability uncertainty

It is the inter-annual variability (IAV) divided by the number of years of valid data in the spliced time series. This results in an uncertainty that reduces as the dataset gets longer.

Consistency uncertainty

A reference data source has a defined consistency uncertainty of 2% which is weighted by the site to spliced data periods ratio.

Synthesis uncertainty

The synthesis uncertainty is the correlation uncertainty weighted by the site to splice data periods ratio. The more of the spliced data that is covered by the site period, the lower the uncertainty is.

Correlation uncertainty

To estimate the uncertainty in the correlation between the site and reference datasets, the correlation dataset is divided in two and one half is used to predict the other and calculate the error. Using a Monte-Carlo approach this method is ran multiple times to obtain an estimate of the uncertainty.

A minimum of 12 concurrent points are necessary.