Shadow Flicker
Shadow flicker is the occurrence of periodic changes in light intensity, due to the shadow of a wind turbine blade passing over a point of interest.
The Shadow Flicker Module simulates the path of the sun during the year and assesses at each time interval the possible shadow flicker at one or multiple receptor position(s). The output of the module can be used to design a wind farm to fulfil planning requirements. The results of the module can also be used to reduce shadow flicker annoyance at the receptors by providing the turbine controller or SCADA system with a time and date of shadow flicker occurrences, so that turbines can be switched off at these times.
Inputs
The following inputs to the WindFarmer model are required to produce an estimate of the shadow flicker effect at the wind farm:
Latitude where the wind farm(s) is located (γ)
Longitude where the wind farm(s) is located (λ)
Time Zone
Minimum elevation angle of the sun
Calculation time interval
Maximum distance from turbine for calculation
Resolution of calculation points
Turbine and shadow receptor locations
Turbine dimensions (hub height, rotor diameter, distance between rotor and turbine tower centre)
Latitude and longitude are derived by WindFarmer directly from the wind farm coordinates.
Methodology of the shadow flicker calculation
Before performing the actual shadow flicker calculation, the program determines the position of the sun at any time of the year. The following definitions and equations are used to determine the elevation and azimuth angle that determine the position of the sun. For more details and definitions, see [26] and [27].
The Hour Angle is the angular displacement of the sun west or east of the local meridian due to the rotation of the earth on its axis at 15° per hour.
In order to obtain the hour angle, the program first calculates:
Julian Date:
Julian Date (JD) is defined as the difference in days between the current Julian day and the Julian day at noon on 1st January 2000:
$$JD = 2432916.5 + 365 \cdot delta + leap + day + \frac{h\textrm{our}}{24}$$
where:
$$delta = year - 1949$$
$$leap = \operatorname{int}\left( \frac{\textrm{delta}}{4} \right)$$
where int is defined as the integer portion of the argument.
Elliptic coordinates:
The elliptic coordinates are the mean longitude (L), mean anomaly (g), ecliptic longitude (l) and obliquity of the ecliptic (ep). These parameters are calculated using the equations:
$$n = JD - 2451545.0$$
$$L = 280.460 + 0.9856474 \cdot n (0° ≤ L < 360°)$$
$$g = 357.528 + 0.9856003 \cdot n (0° ≤ g < 360°)$$
$$l = L + 1.915 \cdot \sin(g) + 0.020 \cdot \sin(2g) (0 ≤ l < 360°)$$
$$ep = 23.439 - 0.0000004 \cdot n$$
Celestial coordinates:
For the calculation of the celestial coordinates (right ascension (ra) and declination (dec)) WindFarmer uses the following equations:
$$\tan(ra) = \cos(ep) \cdot \frac{\sin(l)}{\cos(l)}$$
$$\sin(dec) = \sin(ep) \cdot \sin(l)$$
The next step is to calculate the azimuth angle (az) and elevation (el). To calculate az and el it is necessary to calculate the hour angle, for which we must first calculate the following terms:
Greenwich mean sidereal time (gmst):
The formula to approximate the Greenwich mean sidereal time to an arbitrary time is given by:
$$gmst = 6.697375 + 0.0657098242 \cdot n + hour(UT) (0 ≤ gmst < 24 h)$$
Local mean sidereal time (lmst):
To calculate the local mean sidereal time (lmst) from a given gmst, we just need to add the east longitude to the gmst:
$$lmst = gmst + \frac{\textrm{east.longitude}}{15}$$
Hour angle:
Then the Hour Angle (ha) can be calculated using:
$$ha = lmst - \textrm{ra}) (-12 < ha ≤ 12 h)$$
The Hour Angle is defined as negative before the sun reaches the meridian and positive when it has already reached the postmeridian hemisphere.
Azimuth and Elevation
Finally, to calculate the parameters that define the solar position which are the azimuth (az) and the elevation (el) WindFarmer uses the following equations:
$$\sin(el) = \sin(dec) \cdot \sin(lat) + \cos(dec) \cdot \cos(lat) \cdot \cos(ha)$$
and then the calculation for azimuth angle which is measured from North (0°)
$$\sin(az) = - \cos(dec) \cdot \frac{\sin(ha)}{\cos(el)}) (0° ≤ az < 360°)$$
Occurrence of shadow flicker
The occurrence of shadow flicker is determined by the wind turbine position (point P) and sun position (elevation angle and azimuth angle). The program calculates from these the minimum distance from the wind turbine hub to any point (S) on the line between the sun and the point of interest (A).
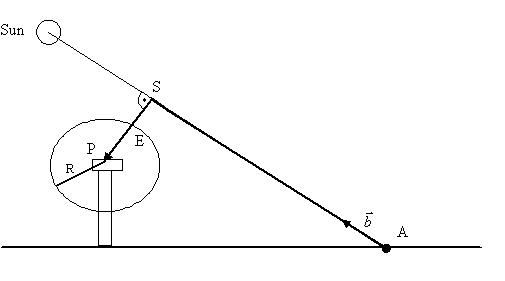
Shadow flicker calculation
Points A, P and S are represented by their vectors $$\overrightarrow{a}$$, $$\overrightarrow{p}$$ and $$\overrightarrow{s} = \overrightarrow{a} + \lambda_{S}\overrightarrow{b}$$
Vector $\overrightarrow{b}$is the unit vector pointing from the receptor to the middle of the sun. It is given by:
$$\overrightarrow{b} = \begin{pmatrix} \cos\left( \textrm{el} \right)\sin\left( \textrm{az} \right) \ \cos\left( \textrm{el} \right)\cos\left( \textrm{az} \right) \ \sin\left( \textrm{el} \right) \ \end{pmatrix}$$
For vector AS to be perpendicular to vector PS we require: $$\overrightarrow{b} \bullet (\overrightarrow{s} - \overrightarrow{p}) = 0$$
This leads to vector SP, perpendicular to vector AS: $$overset{\rightarrow}{\textrm{sp}} = \overrightarrow{a} + \frac{\overrightarrow{b} (\overrightarrow{p} - \overrightarrow{a})}{\overrightarrow{b}\overrightarrow{b}}\overrightarrow{b} - \overrightarrow{p}$$
WindFarmer compares the norm of vector PS with the radius R of the turbine. This is repeated in time intervals of, for example 1 minute, throughout one year, to detect if shadow is produced at the point of analysis, at this time. The program counts the minutes per day and the hours per year of shadow flicker caused by that wind turbine.
WindFarmer always considers the topography in the calculation, using the height ASL specified in the gridded elevations file. WindFarmer optionally allows you to detect if the direct line of sight between receptor and turbine, or between the turbine and the sun is blocked by terrain features.
Modelling the rotor as a disc
If the rotor is modelled as a sphere, this represents the worst possible geometric scenario. This is the method we recommend. Alternative options in WindFarmer allow the rotor to be modelled in a vertical plane of defined orientation.
When the distance between the rotor and the turbine tower centre is taken into account and the rotor disc model is being used, the worst case scenario occurs when the rotor is facing 180 degrees away from the sun’s azimuth.
By taking into account the wind speed and direction frequency distribution, a more likely occurrence of shadow flicker can be derived, as compared with this geometric worst case.
Modelling the sun as a disc
If shadow flicker is calculated by modelling the sun as a disc, vector $\overrightarrow{b}$ points to the edge of the sun’s disc closest to the rotor disc. The sun’s diameter is assumed to be 0.351 degrees.
Please note that current standards and limits assume a point source and that this calculation option, whilst more accurately representing theoretical shadow flicker, should not be selected if the result is to be compared with such a limit.
In this calculation no perception threshold is taken into account.
Distance between rotor and turbine centre
Usually, the turbine positions are defined at the centre of the turbine tower. For the shadow flicker calculation, the position of the rotor is important as the rotor is the source of the shadow flicker. The calculation is very sensitive to changes in the relative position of source and receptor - the distance between the turbine rotor and the tower can become crucially important. WindFarmer calculates the rotor offset using:
$$\textrm{rotor offset} = \frac{1}{2}\textrm{tower top diameter} + \textrm{tower position} + \textrm{disc depth}$$
Tower top diameter, tower position and disc depth are defined in the turbine 3D model for each turbine type.
Notes
The shadow flicker calculation makes the following simplifications:
by default assumes that there are no clouds, but weightings may be assigned in a script to account for cloud cover
that the turbines are always rotating
a limit to human perception of the shadow flicker is not considered